12HashMap

HashMap

---

2022-08-27

计算hashmap规则

/*Computes key.hashCode() and spreads (XORs) higher bits of hash to lower. Because the table uses power-of-two masking, sets of hashes that vary only in bits above the current mask will always collide. (Among known examples are sets of Float keys holding consecutive whole numbers in small tables.) So we apply a transform that spreads the impact of higher bits downward. There is a tradeoff between speed, utility, and quality of bit-spreading. Because many common sets of hashes are already reasonably distributed (so don't benefit from spreading), and because we use trees to handle large sets of collisions in bins, we just XOR some shifted bits in the cheapest possible way to reduce systematic lossage, as well as to incorporate impact of the highest bits that would otherwise never be used in index calculations because of table bounds.*/
static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

将高位再次异或的原因是减少hash碰撞

1.hashmap 的桶是2次方倍

2.Float这类特殊的hashcode计算方式(符号+指数+有效数字)

/*
Returns a representation of the specified floating-point value according to the IEEE 754 floating-point "single format" bit layout, preserving Not-a-Number (NaN) values.
Bit 31 (the bit that is selected by the mask 0x80000000) represents the sign of the floating-point number. Bits 30-23 (the bits that are selected by the mask 0x7f800000) represent the exponent. Bits 22-0 (the bits that are selected by the mask 0x007fffff) represent the significand (sometimes called the mantissa) of the floating-point number.
If the argument is positive infinity, the result is 0x7f800000.
If the argument is negative infinity, the result is 0xff800000.
If the argument is NaN, the result is the integer representing the actual NaN value. Unlike the floatToIntBits method, floatToRawIntBits does not collapse all the bit patterns encoding a NaN to a single "canonical" NaN value.
In all cases, the result is an integer that, when given to the intBitsToFloat(int) method, will produce a floating-point value the same as the argument to floatToRawIntBits.
Params:
value – a floating-point number.
Returns:
the bits that represent the floating-point number.
Since:
1.3
*/
 public static native int floatToRawIntBits(float value);
 
 /*
 Returns a representation of the specified floating-point value according to the IEEE 754 floating-point "single format" bit layout.
Bit 31 (the bit that is selected by the mask 0x80000000) represents the sign of the floating-point number. Bits 30-23 (the bits that are selected by the mask 0x7f800000) represent the exponent. Bits 22-0 (the bits that are selected by the mask 0x007fffff) represent the significand (sometimes called the mantissa) of the floating-point number.
If the argument is positive infinity, the result is 0x7f800000.
If the argument is negative infinity, the result is 0xff800000.
If the argument is NaN, the result is 0x7fc00000.
In all cases, the result is an integer that, when given to the intBitsToFloat(int) method, will produce a floating-point value the same as the argument to floatToIntBits (except all NaN values are collapsed to a single "canonical" NaN value).
Params:
value – a floating-point number.
Returns:
the bits that represent the floating-point number.
 */
   public static int floatToIntBits(float value) {
        int result = floatToRawIntBits(value);
        // Check for NaN based on values of bit fields, maximum
        // exponent and nonzero significand.
        if ( ((result & FloatConsts.EXP_BIT_MASK) ==
              FloatConsts.EXP_BIT_MASK) &&
             (result & FloatConsts.SIGNIF_BIT_MASK) != 0)
            result = 0x7fc00000;
        return result;
    }
    
     public static int hashCode(float value) {
        return floatToIntBits(value);
    }

System.out.println(Integer.toHexString(new Float(1).hashCode()));
System.out.println(Integer.toHexString(new Float(2).hashCode()));
System.out.println(Integer.toHexString(new Float(3).hashCode()));
System.out.println(Integer.toHexString(new Float(4).hashCode()));
System.out.println(Integer.toHexString(new Float(5).hashCode()));
System.out.println(Integer.toHexString(new Float(6).hashCode()));
System.out.println(Integer.toHexString(new Float(7).hashCode()));
System.out.println(Integer.toHexString(new Float(8).hashCode()));
System.out.println(Integer.toHexString(new Float(9).hashCode()));
System.out.println(Integer.toHexString(new Float(10).hashCode()));
System.out.println(Integer.toHexString(new Float(11).hashCode()));
//        3f800000
//        40000000
//        40400000
//        40800000
//        40a00000
//        40c00000
//        40e00000
//        41000000
//        41100000
//        41200000
//        41300000

---

HashMap是由数组，链表，红黑树组成的数据结构

数组里面每个地方都存了Key-Value这样的实例，在Java7叫Entry在Java8中叫Node。

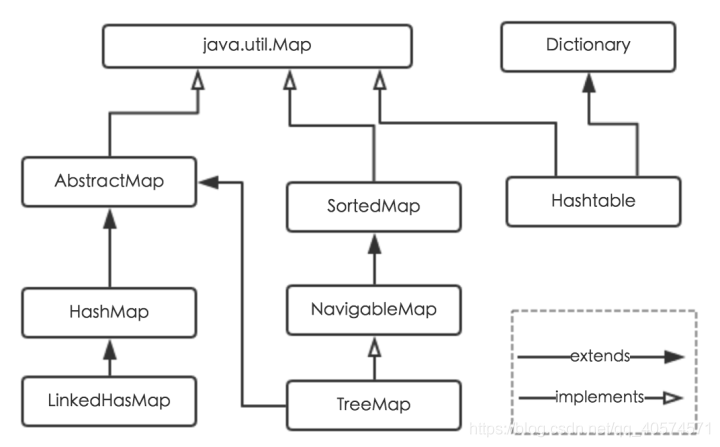
• HashMap：

  • 它根据键的hashCode值存储数据，大多数情况下可以直接定位到它的值，因而具有很快的访问速度，但遍历顺序却是不确定的。 HashMap最多只允许一条记录的键为null，允许多条记录的值为null。HashMap非线程安全，即任一时刻可以有多个线程同时写HashMap，可能会导致数据的不一致。如果需要满足线程安全，可以用 Collections的synchronizedMap方法使HashMap具有线程安全的能力，或者使用ConcurrentHashMap。

  • Collections的synchronizedMap将原来的Map封装成一个新Map,新Map里面所有方法都加上了Synchronize

• Hashtable：

  • Hashtable是遗留类，很多映射的常用功能与HashMap类似，不同的是它承自Dictionary类，并且是线程安全的，任一时间只有一个线程能写Hashtable，并发性不如ConcurrentHashMap，因为ConcurrentHashMap引入了分段锁。Hashtable不建议在新代码中使用，不需要线程安全的场合可以用HashMap替换，需要线程安全的场合可以用ConcurrentHashMap替换。
  • HashTable就是加上了Synchronize

• LinkedHashMap：

  • LinkedHashMap是HashMap的一个子类，保存了记录的插入顺序，在用Iterator遍历LinkedHashMap时，先得到的记录肯定是先插入的，也可以在构造时带参数，按照访问次序排序。

• TreeMap：

  • TreeMap实现SortedMap接口，能够把它保存的记录根据键排序，默认是按键值的升序排序，也可以指定排序的比较器，当用Iterator遍历TreeMap时，得到的记录是排过序的。如果使用排序的映射，建议使用TreeMap。在使用TreeMap时，key必须实现Comparable接口或者在构造TreeMap传入自定义的Comparator，否则会在运行时抛出java.lang.ClassCastException类型的异常。

HashMap数据结构

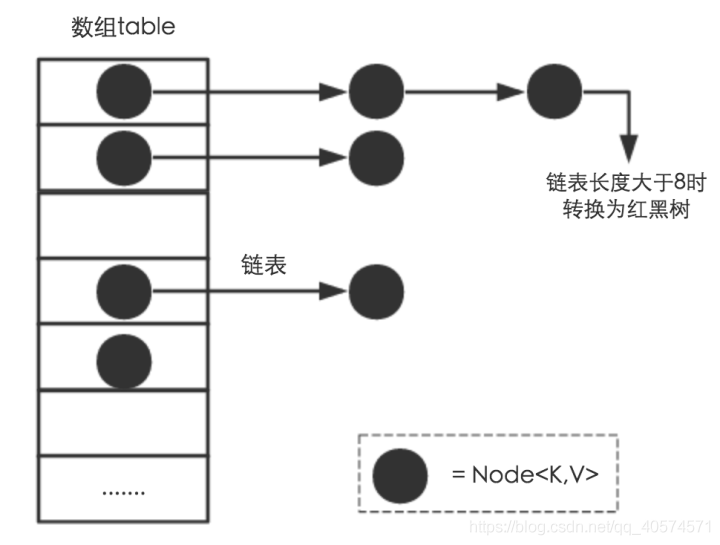
HashMap扩容

Node[] table的初始化长度length(默认值是16)，Load factor为负载因子(默认值是0.75)，threshold是HashMap所能容纳的最大数据量的Node(键值对)个数。threshold = length * Load factor。也就是说，在数组定义好长度之后，负载因子越大，所能容纳的键值对个数越多。

threshold就是在此Load factor和length(数组长度)对应下允许的最大元素数目，超过这个数目就重新resize(扩容)，扩容后的HashMap容量是之前容量的两倍。默认的负载因子0.75是对空间和时间效率的一个平衡选择

相对来说素数导致冲突的概率要小于合数，Hashtable初始化桶大小为11，就是桶大小设计为素数的应用（Hashtable扩容后不能保证还是素数）。HashMap采用这种非常规设计，主要是为了在取模和扩容时做优化，同时为了减少冲突，HashMap定位哈希桶索引位置时，也加入了高位参与运算的过程。

HashMap hash

   static final int hash(Object key) {
       int h;
       return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
   }

if ((p = tab[i = (n - 1) & hash]) == null)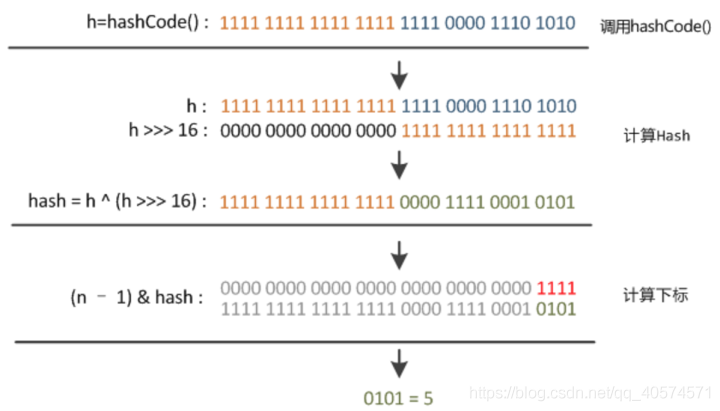

HashMap 线程安全问题

数据不一致

• 如果多个线程同时使用 put 方法添加元素，而且假设正好存在两个 put 的 key 发生了碰撞（根据 hash 值计算的 bucket 一样），那么根据 HashMap 的实现，这两个 key 会添加到数组的同一个位置，这样最终就会发生其中一个线程 put 的数据被覆盖
• 如果多个线程同时检测到元素个数超过数组大小 * loadFactor，这样就会发生多个线程同时对 Node 数组进行扩容，都在重新计算元素位置以及复制数据，但是最终只有一个线程扩容后的数组会赋给 table，也就是说其他线程的都会丢失，并且各自线程 put 的数据也丢失

死循环（1.7头插法）

使用头插会改变链表的上的顺序，但是如果使用尾插，在扩容时会保持链表元素原本的顺序，就不会出现链表成环的问题了。

1.8改成尾插法后没有死循环问题

部分代码

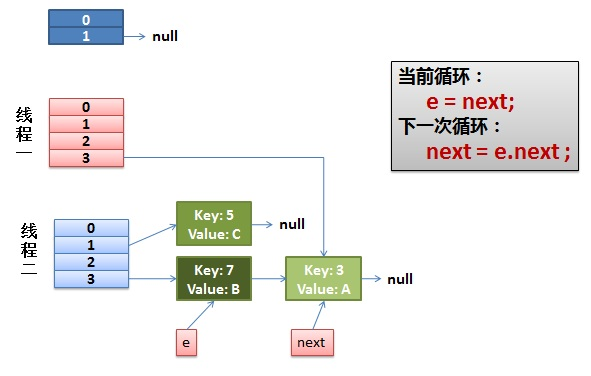
do {
             Entry<K,V> next = e.next;//假如有一个线程在这里停住了
             int i = indexFor(e.hash, newCapacity);
             e.next = newTable[i]; 
             newTable[i] = e; 
             e = next;
         } while (e != null);

头插法正常逻辑

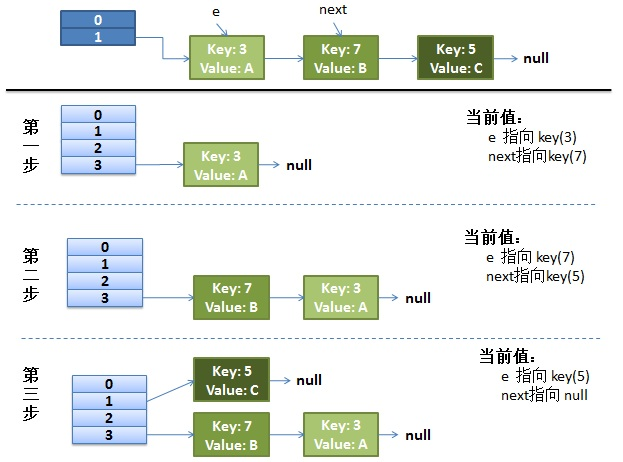
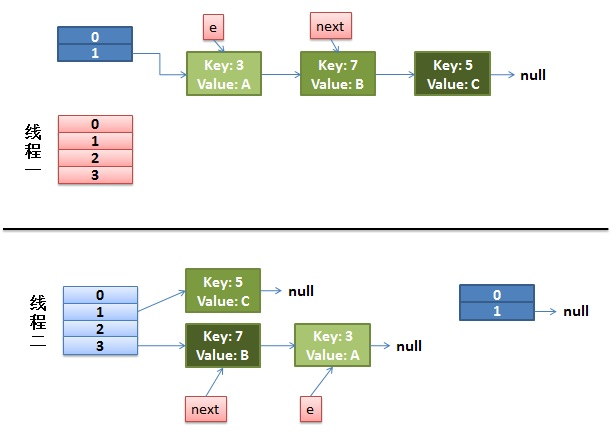
并发下插入

线程一在 Entry<K,V> next = e.next;位置停住了

线程二，完成了rehash

线程一重新被调度回来运行

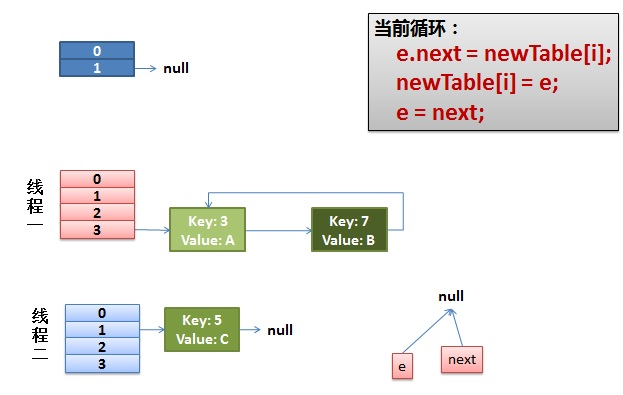
最终造成死循环

Spliterator

HashMap 内部类分割迭代器 HashMapSpliterator、KeySpliterator、ValueSpliterat、EntrySplitera

static class MyThread implements Runnable {
    Spliterator<Integer> spliterator;
    String threadName;
    
    MyThread(Spliterator<Integer> spliterator, String threadName) {
        this.spliterator = spliterator;
        this.threadName = threadName;
    }
    @Override
    public void run() {
        spliterator.forEachRemaining(s -> {
            System.out.println(threadName + "=" + s);
        });
    }
}
public static void main(String[] args) {
    HashMap<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < 23; i++) {
        map.put(i, i);
    }
    Spliterator<Integer> s1 = map.keySet().spliterator();
    Spliterator<Integer> s2 = s1.trySplit();
    Spliterator<Integer> s3 = s2.trySplit();
    
    Thread t1 = new Thread(new MyThread(s1, "线程1"));
    Thread t2 = new Thread(new MyThread(s2, "线程2"));
    Thread t3 = new Thread(new MyThread(s3, "线程3"));
    t1.start();
    t2.start();
    t3.start();
}

线程2=8
线程2=9
线程2=10
线程2=11
线程2=12
线程2=13
线程2=14
线程1=16
线程2=15
线程3=0
线程1=17
线程1=18
线程1=19
线程1=20
线程1=21
线程3=1
线程1=22
线程3=2
线程3=3
线程3=4
线程3=5
线程3=6
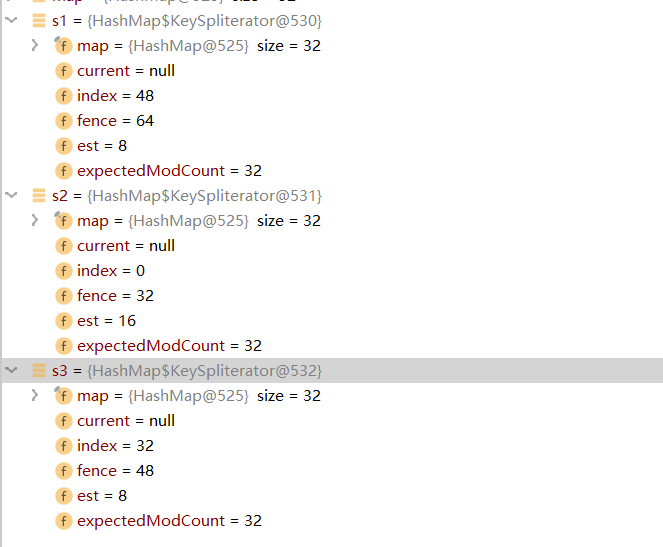
线程3=7

不是均分！！！！！！！！！

假如map的长度为64

按照bucket一次除二

假如分为3份

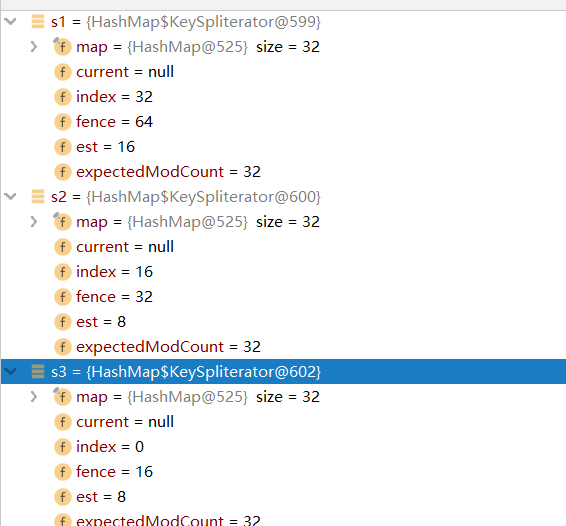
Spliterator<Integer> s1 = map.keySet().spliterator();
   Spliterator<Integer> s2 = s1.trySplit();
   Spliterator<Integer> s3 = s2.trySplit();

s1=> 32—–64

s2-> 16——32

s3-> 0——16

假如分3份

Spliterator<Integer> s1 = map.keySet().spliterator();
Spliterator<Integer> s2 = s1.trySplit();
Spliterator<Integer> s3 = s1.trySplit();

s1=> 48—–64

s2-> 0——32

s3-> 32——48

HashMap 异常（fail-fast）

在put等会改变Map的操作中都会 modCount++

在所有的Iterator ,和foreach中都会判断

所以多线程不能修改，使用线程安全的集合

在单线程中foreach不能修改，在Iterator中可以使用iterator.remove()方法，该方法会更新expectedModCount

//foreach中
int mc = modCount;
for (int i = 0; i < tab.length; ++i) {
    for (Node<K,V> e = tab[i]; e != null; e = e.next)
        action.accept(e.key);
}
if (modCount != mc)
    throw new ConcurrentModificationException();

HashMap指定初始容量

 public HashMap(int initialCapacity, float loadFactor) {
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                                               initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                                               loadFactor);
        this.loadFactor = loadFactor;
        this.threshold = tableSizeFor(initialCapacity);
    }


//该方法就是把第一个不为0的位后面都变成1   +1就是比这个数大的第一个二次幂
 static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

LinkedHashMap LRU

LRU，即：最近最少使用淘汰算法（Least Recently Used）。LRU是淘汰最长时间没有被使用的页面。

LFU，即：最不经常使用淘汰算法（Least Frequently Used）。LFU是淘汰一段时间内，使用次数最少的页面。

//实现LRU
//使用LinkedHashMap实现
//LinkedHashMap底层就是用的【HashMap 加 双链表】实现的，而且本身已经实现了按照访问顺序的存储。
//此外，LinkedHashMap中本身就实现了一个方法removeEldestEntry用于判断是否需要移除最不常读取的数，
//方法默认是直接返回false，不会移除元素，所以需要重写该方法,即当缓存满后就移除最不常用的数。

public class LRU<K,V> {
    private LinkedHashMap<K, V> map;
    private int cacheSize;

    public LRU(int cacheSize)
    {
        this.cacheSize = cacheSize;
        map = new LinkedHashMap<K,V>(16,0.75F,true){

            @Override
            protected boolean removeEldestEntry(Entry eldest) {
                if(cacheSize + 1 == map.size()){
                    return true;
                }else{
                    return false;
                }
            }
        };  //end map
    }

    public synchronized V get(K key) {
        return map.get(key);
    }
    public synchronized void put(K key,V value) {
        map.put(key, value);
    }
    public synchronized void clear() {
        map.clear();
    }
    public synchronized int usedSize() {
        return map.size();
    }
    public void print() {
        for (Map.Entry<K, V> entry : map.entrySet()) {
            System.out.print(entry.getValue() + "--");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        LRU<String, Integer> LRUMap = new LRU<>(3);
        LRUMap.put("key1", 1);
        LRUMap.put("key2", 2);
        LRUMap.put("key3", 3);
        LRUMap.print();
        System.out.println(LRUMap.get("key2"));
        LRUMap.put("key4", 4);
        LRUMap.print();
    }
}

LinkedHashMap
/////////////////////////////
 /**
     * Constructs an empty <tt>LinkedHashMap</tt> instance with the
     * specified initial capacity, load factor and ordering mode.
     *
     * @param  initialCapacity the initial capacity
     * @param  loadFactor      the load factor
     * @param  accessOrder     the ordering mode - <tt>true</tt> for
     *         access-order, <tt>false</tt> for insertion-order
     * @throws IllegalArgumentException if the initial capacity is negative
     *         or the load factor is nonpositive
     */
    public LinkedHashMap(int initialCapacity,
                         float loadFactor,
                         boolean accessOrder) {
        super(initialCapacity, loadFactor);
        this.accessOrder = accessOrder;
    }

public V get(Object key) {
        Node<K,V> e;
        if ((e = getNode(hash(key), key)) == null)
            return null;
            //access为传入第三个参数
        if (accessOrder)
            afterNodeAccess(e);
        return e.value;
    }

    /**
     * {@inheritDoc}
     */
    public V getOrDefault(Object key, V defaultValue) {
       Node<K,V> e;
       if ((e = getNode(hash(key), key)) == null)
           return defaultValue;
       if (accessOrder)
           afterNodeAccess(e);
       return e.value;
   }

//移动到链表结尾
void afterNodeAccess(Node<K,V> e) { // move node to last
        LinkedHashMap.Entry<K,V> last;
        if (accessOrder && (last = tail) != e) {
            LinkedHashMap.Entry<K,V> p =
                (LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
            p.after = null;
            if (b == null)
                head = a;
            else
                b.after = a;
            if (a != null)
                a.before = b;
            else
                last = b;
            if (last == null)
                head = p;
            else {
                p.before = last;
                last.after = p;
            }
            tail = p;
            ++modCount;
        }
    }


//删除链表第一个
 void afterNodeInsertion(boolean evict) { // possibly remove eldest
        LinkedHashMap.Entry<K,V> first;
        if (evict && (first = head) != null && removeEldestEntry(first)) {
            K key = first.key;
            removeNode(hash(key), key, null, false, true);
        }
    }

//被重写方法
prot boolean removeEldestEntry(Map.Entry<K,V> eldest) {
        return false;
    }