04缺失的第一个正数

缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例 1：

输入：nums = [1,2,0]
输出：3
解释：范围 [1,2] 中的数字都在数组中。

示例 2：

输入：nums = [3,4,-1,1]
输出：2
解释：1 在数组中，但 2 没有。

示例 3：

输入：nums = [7,8,9,11,12]
输出：1
解释：最小的正数 1 没有出现。

提示：

• 1 <= nums.length <= 105
• -231 <= nums[i] <= 231 - 1

对于一个长度为 N 的数组，其中没有出现的最小正整数只能在 [1,N+1] 中。这是因为如果 [1,N] 都出现了，那么答案是 N+1，否则答案是 [1,N] 中没有出现的最小正整数

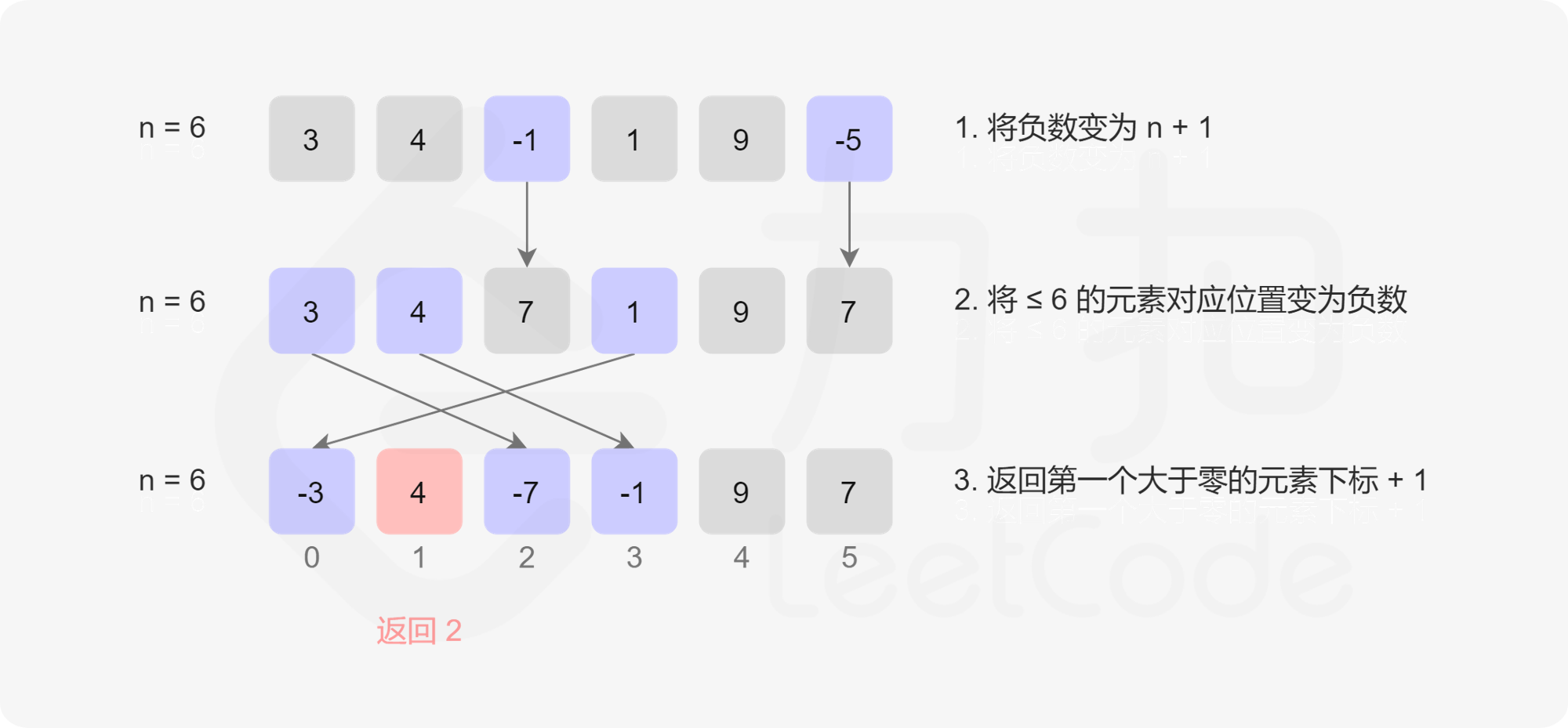
• 将数组中所有小于等于 0 的数修改为 N+1；

• 遍历数组中的每一个数 x，它可能已经被打了标记，因此原本对应的数为 ∣x∣，其中 ∣∣ 为绝对值符号。如果 ∣x∣∈[1,N]，那么我们给数组中的第 ∣x∣−1 个位置的数添加一个负号。注意如果它已经有负号，不需要重复添加；

• 在遍历完成之后，如果数组中的每一个数都是负数，那么答案是 N+1，否则答案是第一个正数的位置加 1

public int firstMissingPositive(int[] nums) {
  int n = nums.length;
  for (int i = 0; i < n; ++i) {
    if (nums[i] <= 0) {
      nums[i] = n + 1;
    }
  }
  for (int i = 0; i < n; ++i) {
    int num = Math.abs(nums[i]);
    if (num <= n) {
      nums[num - 1] = -Math.abs(nums[num - 1]);
    }
  }
  for (int i = 0; i < n; ++i) {
    if (nums[i] > 0) {
      return i + 1;
    }
  }
  return n + 1;
}